martes, 28 de abril de 2015
viernes, 17 de abril de 2015
jueves, 16 de abril de 2015
Aurora Borealis
Un imán colgado o una brújula apuntan al norte porque la Tierra misma es un gigantesco imán. La brújula se alinea con el campo magnético de la Tierra. Sin embargo, los polos magnéticos terrestres no coinciden con los polos geográficos. La discrepancia entre la orientación de una brújula y el norte verdadero se llama declinación magnética.
Sea cual fuere la causa, el campo magnético terrestre no es estable; ha variado durante el tiempo geológico. La prueba de ello se encuentra en los análisis de las propiedades magnéticas de los estratos rocosos.
El Universo es un campo de tiro de partículas cargadas, las cuales se llaman rayos cósmicos y consisten en protones, partículas alfa y otros núcleos atómicos, así como electrones de alta energía. Los protones podrían ser restos del Big Bang, en cualquier caso, viajan por el espacio con rapideces fantásticas, y forman la radiación cósmica, tan peligrosa para los astronautas. Dicha radiación se intensifica cuando el Sol está activo y aporta sus propias partículas cargadas. Los rayos cósmicos también son un peligro para la instrumentación electrónica en el espacio: los impactos de núcleos de rayos cósmicos muy ionizantes pueden causar ¨inversiones¨ en los bits de la memoria de las computadoras, o la falla de microcircuitos. Por fortuna, para nosotros en la superficie terrestre, la mayoría de esas partículas cargadas se desvían y alejan gracias al campo magnético de nuestro planeta. Algunas de ellas quedan atrapadas en los confines externos del campo magnético y forman los cinturones de radiación de Van Allen.
La mayoría de las partículas cargadas probablemente vienen del Sol. Las tormentas solares lanzan partículas cargadas hacia afuera, como surtidores gigantescos, y muchas de ellas pasan cerca de la Tierra y quedan atrapadas por el campo magnético. Las partículas cargadas describen trayectorias en forma de espiral, en torno a las líneas del campo magnético terrestre, y regresan o rebotan, entre los polos magnéticos terrestres, a mucha altura sobre la atmósfera. Las perturbaciones del campo terrestre permiten, con frecuencia que los iones se sumerjan en la atmósfera y hagan que brille como una lámpara fluorescente. Son las bellas aurora boreal en el hemisferio norte, y aurora austral en el hemisferio sur.
Es probable que las partículas atrapadas en el cinturón interno se hayan originado en la atmósfera terrestre. Las explosiones de bombas de hidrógeno a gran altitud, en 1962, aportaron electrones frescos a este cinturón.
A pesar del campo magnético terrestre protector, muchos rayos cósmicos ¨secundarios¨ llegan a la superficie terrestre. Son partículas formadas cuando los rayos cósmicos ¨primarios¨, los que provienen del espacio exterior, chocan contra núcleos atómicos en la alta atmósfera. El bombardeo de los rayos cósmicos es máximo en los polos magnéticos, porque las partículas cargadas que chocan contra la Tierra en esos lugares no viajan a través de las líneas del campo magnético, sino a lo largo de las líneas y no se desvían. El bombardeo disminuye al alejarse de los polos y es mínimo en las regiones ecuatoriales.
Referencia: Física Conceptual de Paul HewittMath + Music

El gran matemático, y no sólo matemático, Gottfried Leibniz, dijo en una ocasión que la música era el placer que experimenta la mente humana al contar sin darse cuenta de que está contando. Obviamente se debe entender esta afirmación en el marco de la estrecha relación existente entre música y matemáticas, pues son muchas y verdaderamente fascinantes las conexiones que hay entre ellas: las relaciones entre los sonidos de un acorde, los fenómenos de resonancia, las claves secretas de la partitura, el compás, las métricas, los ritmos, intervalos, las estructuras geométricas, la relación entre armonía y número que tanto asombró a los pitagóricos, o las ingeniosas técnicas de repetición y traslación empleadas por Bach, Mozart y otros muchos compositores en sus obras maestras.
miércoles, 15 de abril de 2015
Matemáticas y Química: una relación necesaria
No sé si las matemáticas necesitan a la química. De lo que estoy convencido es que la química necesita a las matemáticas. La situación actual de la química, sus relaciones históricas con otras
ciencias, especialmente con la física, su relación actual con las
matemáticas, destacando lo mucho que las matemáticas están aportando
actualmente a la química en el área de la química computacional,
especialmente en la cuantificación de la aromaticidad a través de las
redes neuronales, una herramienta de las matemáticas computacionales con
aplicaciones en múltiples campos (metereología, economía, ciencias
computacionales, etc.) en los que se manejan cantidades enormes de
datos. Además, la química puede aportar al futuro bienestar de la humanidad, así como el
papel que las matemáticas pueden tener en el futuro de la química; y,
por lo tanto, de la humanidad.
Lo que ya es una evidencia en la literatura científics: la interacción
entre la química y las matemáticas está creando un área científica
multidisciplinar, que está adquiriendo una gran relevancia científica,
especialmente para la química.
La química como la ciencia central que interacciona con
otras ciencias, desde la física hasta la geología o la agricultura (ver
imagen). Esta centralidad de la química significa que muchas veces la
otra ciencia usa métodos y materiales (proporcionados por la química)
para realizar avances (¿se pueden imaginar los avances en biología molecular o biomedicina sin el empleo de sustancias químicas?).
Este aspecto se ve reflejado por el sentido de la flecha que une a la
química a la otra ciencia. Por otro lado, la centralidad de la química
también se manifiesta cuando dos ciencias aparentemente lejanas
interaccionan entre ellas; frecuentemente lo tienen que hacer a nivel
íntimo de la materia, es decir a través de átomos y moléculas, el
terreno de la química.
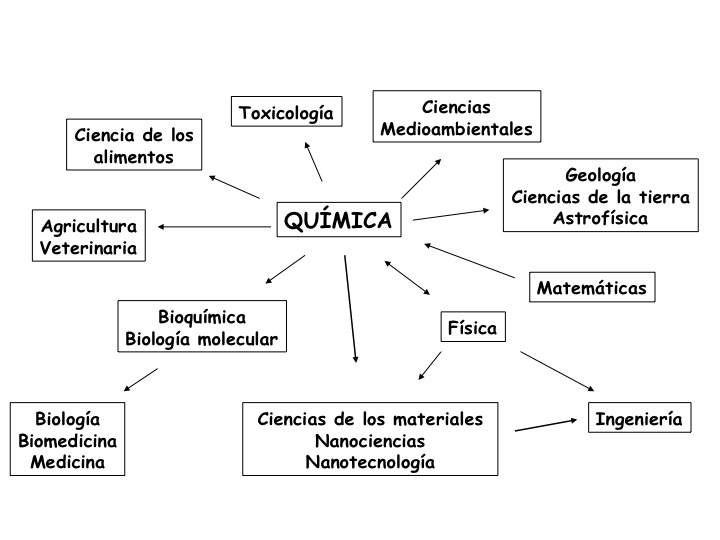

La relación de la química con la física
es algo especial. Como se observa en la figura, la flecha que une estas
dos ciencias es de doble punta. Esto significa que la químca hace
aportaciones a la física (como las indicadas en el párrafo anterior),
pero la física proporciona la mayor parte del bagaje teórico de la
química.
Y ¿qué pasa con la relación entre la química y las matemáticas?
El sentido de la flecha es desde las matemáticas a la química; lo que
significa que la química prácticamente no ha hecho aportaciones a las
matemáticas. La química indudablemente usa las matemáticas
continuamente. En la imagen siguiente se indican algunas de las
aportaciones de las matemáticas a la química, tanto actuales (en azul)
como esperables (en rojo).

Sin embargo, ¿qué tipo de uso hace la química de las matemáticas? ¿Qué responderían los químicos si les preguntásemos si necesitan las matemáticas para su investigación? La mayoría, independientemente del área (considero sólo las 4 grandes y clásicas divisiones de la química: analítica, física, inorgánica y orgánica), responderían que usan las matemáticas para hacer cálculos (estequiometría, rendimientos, despejar alguna incógnita, etc.; es decir, aritmética y álgebra elementales), algún ajuste estadístico (principalmente los químicos analíticos interesados en quimiometría), y algún químico-físico podrá decir que unas matemáticas “más sofisticadas” (un poco de análisis matemático) para explicar los resultados experimentales o avanzar en aspectos teóricos.
Desde mediados del siglo XIX,
especialmente debido al gran desarrolo de la síntesis orgánica, la
química ha proporcionado infinidad de sustancias con las que se han
hecho los materiales que facilitan nuestra existencia, desde
medicamentos hasta material para electrónica, pasando por alimentos,
ropa y energía, entre otros. Estos enormes avances indican que la
química es una ciencia madura capaz de obtener prácticamente todo lo que
se proponga.
Sin embargo, aunque parezca contradictiorio, la química es, en cierto sentido, una ciencia aún inmadura;
con muchos conceptos fundamentales pendiente de ser definidos y
cuantificado de manera rigurosa. Algunos de estos conceptos son los
siguientes: estructura química (sabemos dibujarla, determinarla y un montón de cosas más, pero nos falta fundamento), orbital (¿existen realmente? y si existen, ¿qué significa?), enlace (¿de dónde procede su estabilidad?), electronegatividad, conjugación, aromaticidad, hiperconjugación, efectos estereoelectrónicos, periodicidad de las propiedades químicas (tenemos que explicar mejor la Tabla Periódica), efectos relativistas, y muchos más.
Cunado establezcamos los fundamentos
sólidos de la química, seremos capaces de decidir si la química es
realmente una ciencia autónoma o es, más bien, una parte de la física. Y
además, podremos preguntarnos si, por similitud con la física y las
matemáticas, ¿existe una filosofía química? Esta pregunta está
relacionada con un aspecto importante de la filosofía de la ciencia.
Creo que las matemáticas pueden ayudar a establecer estos conceptos fundamentales. Para ello, tenemos que conseguir la matematización de la química.
Otros beneficios de esta relación será que la química podrá explicar
mejor los resultados experimentales y tendrá mayor capacidad de
predición de las propiedades de las moléculas y de los materiales que
con ellas se fabriquen.
Ahora sólo falta que los químicos
proporcionemos temas interesantes de investigación a los matemáticos y
que la flecha que une las dos ciencais sea de doble punta.
Nota. Esta entrada participa en la 3,14159 Edición del Carnaval de Matemáticas que aloja José Lopez Nicolás en su blog Scientia; y en la XVI Edición del Carnaval de Química que aloja Dr. Litos en su blog.
Bernardo Herradón García CSIC
b.herradon@csic.es
Referencia: https://educacionquimica.wordpress.com
martes, 14 de abril de 2015
Suscribirse a:
Comentarios (Atom)